Cornell University
School of Civil & Environmental Engineering
CEE 6570 — Biological Processes
© James M. Gossett (March 25, 2012)
BIOENERGETICS & STOICHIOMETRY**
(An excerpt from class notes)
I. INTRODUCTION
Classical thermodynamic concepts, along with some observations of the efficiency with which bacteria capture free energy, can be used to predict cell yields and the overall stoichiometry associated with growth. Cell yields are useful for predicting biological sludge production in microbial processes. Stoichiometries allow estimation of a number of important factors: nutrient requirements; effects of growth on alkalinity and pH; and composition of gas evolved in anaerobic processes.
We begin with the definition of an “electron equivalent” — a unit of expression which is particularly convenient in subsequent derivations.
Definition:
1 electron equivalent (eeq) of some electron donor (e.d.) = amount of the substance which releases 1 mol e– during a specified oxidation reaction.
Thus, the molar quantity which corresponds to 1 eeq is reaction dependent. For example, consider the oxidation of elemental iron (Fe). We may write its oxidation to ferrous form:
1/2 Fe --> 1/2 Fe+2 + e–
from which we would conclude that 1 eeq Fe = 1/2 mol Fe. On the other hand, if oxidation were complete to ferric form, the appropriate oxidation half-reaction would be
1/3 Fe --> 1/3 Fe+3 + e–
in which 1 eeq Fe = 1/3 mol Fe. Or, we might even be interested in the oxidation of ferrous (Fe+2) to ferric (Fe+3) form, in which 1 eeq Fe = 1 mol Fe.
In this course, we shall attempt to remove ambiguity — at least for organic electron donors — by universally defining electron equivalents in terms of total carbonaceous oxidation:
1 eeq of organic electron donor = amount of the substance which releases 1 mol e– during total carbonaceous oxidation (i.e., --> CO2, NH4+). In other words, proteinaceous nitrogen (–III oxidation state) is not oxidized, but is released as ammonia (also –III oxidation state).
Table 1 depicts oxidation half-reactions for a number of organic electron donors (e.d.), each written as a complete carbonaceous oxidation [Rxns (7) through (17)]. Thus,
1 eeq acetate = 1/8 mol acetate
1 eeq glucose = 1/24 mol C6H12O6
etc.
TABLE 1. OXIDATION HALF REACTIONS
∆Go(w)
HALF REACTIONS kcal/eeq*
Reactions for Bacterial Cell Synthesis (Rc)
Ammonia as Nitrogen Source:
1. 1/20 C5H7O2N + 9/20 H2O = 1/5 CO2 + 1/20 HCO3– + 1/20 NH4+ + H+ + e–
Nitrate as Nitrogen Source:
2. 1/28 C5H7O2N + 11/28 H2O = 1/28 NO3– + 5/28 CO2 + 29/28 H+ + e–
Reactions for Electron Acceptors (Ra)
Oxygen:
3. 1/2 H2O = 1/4 O2 + H+ + e– 18.675
Nitrate:
4. 1/10 N2 + 3/5 H2O = 1/5 NO3– + 6/5 H+ + e– 17.128
Sulfate:
5. 1/16 H2S + 1/16 HS– + 1/2 H2O = 1/8 SO4= + 19/16 H+ + e– –5.085
Carbon Dioxide:
6. 1/8 CH4 + 1/4 H2O = 1/8 CO2 + H+ + e– –5.763
Reactions for Electron Donors (Rd)
Organic Donors
Domestic Wastewater:
7. 1/50 C10H19O3N + 9/25 H2O = 9/50 CO2 + 1/50 NH4+ + 1/50 HCO3– + H+ + e– –7.6
Protein:
8. 1/66 C16H24O5N4 + 27/66 H2O = 8/33 CO2 + 2/33 NH4+ + 31/33 H+ + e– –7.7
Carbohydrate (Cellulose, Starch, Sugars):
9. 1/24 C6H12O6 + 1/4 H2O = 1/4 CO2 + H+ + e– –10.0
Grease, Fat, and Oil:
10. 1/46 C8H16O + 15/46 H2O = 4/23 CO2 + H+ + e– –6.6
Acetate:
11. 1/8 CH3COO– + 3/8 H2O = 1/8 CO2 + 1/8 HCO3– + H+ + e– –6.609
Propionate:
12. 1/14 CH3CH2COO– + 5/14 H2O = 1/7 CO2 + 1/14 HCO3– + H+ + e– –6.664
Benzoate:
13. 1/30 C6H5COO– + 13/30 H2O = 1/5 CO2 + 1/30 HCO3– + H+ + e– –6.892
Ethanol:
14. 1/12 CH3CH2OH + 1/4 H2O = 1/6 CO2 + H+ + e– –7.592
Lactate:
15. 1/12 CH3CHOHCOO– + 1/3 H2O = 1/6 CO2 + 1/12 HCO3– + H+ + e– –7.873
Pyruvate:
16. 1/10 CH3COCOO– + 2/5 H2O = 1/5 CO2 + 1/10 HCO3– + H+ + e– –8.545
Methanol:
17. 1/6 CH3OH + 1/6 H2O = 1/6 CO2 + H+ + e– –8.965
* 25ŻC; reactants and products at unit activity, except {H} = 10–7 (i.e, pH 7 conditions).
For organic electron donors, we will adopt a definition of eeq based on complete carbonaceous oxidation — regardless of whether the actual microbial decomposition is complete. This means that 1 eeq glucose will always represent 1/24 mol — whether glucose is completely oxidized by aerobic bacteria (--> CO2, H2O), or merely fermented to lactate in the absence of oxygen.
It is also worth mentioning that — since our definition of eeq is based on complete carbonaceous oxidation — then
1 eeq of any organic e.d. = 8 g COD
The reason: COD (chemical oxygen demand) is the quantity of oxygen required to completely oxidize the carbonaceous portion of an organic compound. If 1 eeq of an organic releases 1 mol e– in complete carbonaceous oxidation, then from Rxn (3) (Table 1), it is apparent that 1/4 mol of O2 (8 g) would be consumed in accepting the 1 mol e–.
For inorganic donors, the definition of “eeq” will necessarily remain reaction-dependent. For example, 1 eeq of ammonia equals either 1/8 or 1/6 mol, depending upon whether one is referring to its oxidation to nitrate [Rxn (19)] or nitrite [Rxn (20)].
For bacterial cell synthesis, we will also adopt reaction-specific definitions of “eeq” which depend upon the datum of nitrogen:
Ammonia as N-Source [Reaction (1)]
1 eeq cells = 1/20 mol C5H7O2N
= 1/20 (113 g VSS) = 5.65 g VSS
= 8 g COD
Nitrate as N-Source [Reaction (2)]
1 eeq cells = 1/28 mol C5H7O2N
= 1/28 (113 g VSS) = 4.04 g VSS
The yield of cells is closely related to the energy content of the electron donor (substrate) supplied and the electron acceptor provided.
II. HETEROTROPHIC
METABOLISM
McCarty’s theories are on relatively firm theoretical ground with respect to heterotrophic metabolism — particularly heterotrophic metabolism in which ammonia serves as N-source. We’ll concentrate first on the application of bioenergetics to estimation of yield coefficients and growth stoichiometries for heterotrophic microorganisms. Later, we’ll extend the application to autotrophic microorganisms, which involves some considerable uncertainties.
Consider what occurs in microbial metabolism: energy is made available to the microorganism via catabolism, energy which is needed for biosynthesis (anabolism) and for mechanical work (e.g., motility, transport of molecules, etc).

In heterotrophic, respiratory microorganisms, we may write — in a sort of shorthand — the following set of equations to represent the production and use of energy in respiration and synthesis, respectively:

where
(ed)red = the reduced form of the electron donor — in this case, some organic substrate (e.g., glucose);
(ea)ox = the oxidized form of the electron acceptor (e.g, O2);
(ed)ox = the oxidized form of the electron donor (e.g., CO2);
(ea)red = the reduced form of the electron acceptor (e.g., H2O);
C5H7O2N = empirical formula for the major elements of bacterial VSS.
In essence, the electron donor (ed) becomes oxidized and the electron acceptor (ea) is reduced. Energy is captured (e.g., as ATP) for use in biosynthesis, which in the case of heterotrophs, involves converting this same electron donor to cellular constituents (C5H7O2N)
When the same electron donor is utilized for both energy and synthesis, we may consider that a fraction of all the donor consumed is used for synthesis, while the remainder fraction is used for energy:
fs = fraction of electron donor used for synthesis;
fe = fraction of electron donor used for energy.
fs + fe = 1
fs and fe depend, of course, on energetics (i.e., the energy available from the respiration reaction, in comparison to that required by the synthesis reaction). But fs and fe also depend upon solids retention time, SRT or "theta_c." As SRT increases (i.e., as net specific growth rate, Ķ, decreases), proportionately more of the electron-donor substrate is consumed to satisfy basal metabolic needs (i.e., the correction to gross growth caused by maintenance or “decay” becomes ever-more significant):

Consequently, fs declines as SRT increases. As we shall see later, fe and fs determine the overall stoichiometry of growth.
A. Energetics — Definitions
Consider the flows of electron donor (ed), electron acceptor (ea), and energy involved in the production of 1 eeq of bacterial cells.
Definitions:
1. ∆Gr
= free energy released per eeq of electron-donor substrate converted for energy (e.g., respiration).
Example: Consider the aerobic utilization of glucose. From the half-reactions of Table 1, we may generate the overall reaction for aerobic catabolism of glucose by subtracting Rxn (3) from Rxn (9) as follows:
∆Go(w)#
(kcal/eeq)
Rxn (9) 1/24 C6H12O6 + 1/4 H2O = 1/4 CO2 + H+ + e– –10.0
–Rxn (3) 1/4 O2 + H+ + e– = 1/2 H2O –18.675
1/24 C6H12O6 + 1/4 O2 = 1/4 CO2 + 1/4 H2O –28.675

2. e
= efficiency of energy transfer to or from the energy carrier (e.g., ATP).
McCarty assumed e = 0.6, a value which resulted in good agreement between his bioenergetic method and experimentally observed stoichiometries.
3. ∆Gs
= carrier (ATP) energy required to synthesize 1 eeq of cells from whatever the carbon and nitrogen sources are. ∆Gs includes energy losses incurred in using ATP energy for synthesis. In other words, more ATP energy is spent in synthesis than the mere thermodynamically calculated value. Additional carrier energy is required because some fraction [presumably (1-e)] will be lost due to biochemical inefficiency. Note the position of the ∆Gs label in the accompanying energy-flow scheme. ∆Gs represents the actual debit on the ATP pool caused by the synthesis of 1 eeq cells, even though only e∆Gs is actually “delivered” to synthesis.
4. A
= eeq of e.d. converted to energy per eeq of cells synthesized — ignoring decay or maintenance.
B. Energy Balance
For the moment, ignore maintenance (decay). It’s OK to do so because what we seek is a means of estimating Y, which itself ignores decay. (Recall that in growth models, we include decay or maintenance through use of a separate b term for it,
dXa/dt = Y(dF/dt) – bXa
where Y represents the stoichiometric relation between gross growth and substrate utilization. Thus, strictly speaking, Y ignores decay and/or maintenance.)
∆Gs kcal of ATP energy is required to form 1 eeq of cells. To replace this amount of ATP energy, the catabolic, ∆Gr reaction must be run A times. Simple thermodynamics tells us that such will potentially yield A∆Gr kcal. However, because of inefficiencies, only eA∆Gr kcal will be captured in the form of ATP. (The difference, [1-e]A∆Gr kcal, is “lost,” appearing as waste biological heat. It, along with similar losses accompanying synthesis and maintenance activities, is what keeps your body at 98.6ŻF and what makes compost piles warm!).
Thus, at steady-state, a bacterium must be replacing ATP at the rate it’s using ATP. Consequently,
eA∆Gr + ∆Gs = 0
where you’ll note that we add the two terms because ∆Gr < 0, while ∆Gs > 0. Solving for A gives,
![]() eeq e.d. to energy
per eeq cells synthesized.
eeq e.d. to energy
per eeq cells synthesized.
We’re interested in A because, as shall be seen, it relates directly to the yield coefficient, Y. We have an estimate of e (i.e., 0.6), and we can easily calculate ∆Gr values from combinations of appropriate half-reactions (Table 1). But arriving at ∆Gs values is a bit trickier, and requires us to invoke some knowledge of biochemical pathways — along with some assumptions.
The ATP energy required for synthesis (∆Gs) is dependent upon the energy state of the carbon source and that of the nitrogen source.
1. Ammonia as Nitrogen Source
Let us first restrict discussion to heterotrophic systems in which ammonia is the N-source. McCarty hypothesizes that synthesis can be divided into two steps:
a) Conversion of the C-source (whatever it is) into some universal intermediate, a compound occupying a central position at what amounts to a grand “intersection” of metabolic pathways. For calculation purposes, McCarty chose pyruvate as that central intermediate — a compound which indeed occupies a prominent position among the highways and byways of metabolism.
∆Gp = free energy required (or evolved) in conversion of the C-source to pyruvate (kcal/eeq pyruvate).
∆Gp is merely the calculated free energy exchanged in conversion to pyruvate. The resulting effect on the ATP pool will either be e∆Gp (if ∆Gp < 0) or ∆Gp/e (if ∆Gp > 0).
b) Conversion of pyruvate and NH4+ to 1 eeq biomass (1/20 C5H7O2N);
∆Gc = ATP energy required to form 1/20 C5H7O2N from pyruvate and ammonia @ 7.5 kcal.
McCarty estimated ∆Gc from studies (by others) in which cellular yields from pyruvate and ammonia were measured. Results indicated an average of 10.5 grams dry biomass solids formed per mol ATP consumed. Assuming dry biomass solids are 90% VSS, and that there are 12.5 kcal available per mol ATP-->ADP under physiological conditions, then ∆Gc = +7.5 kcal ATP/eeq cells (if NH4+ is N-source).
Putting the two steps together then gives
![]()
m = +1 (∆Gp > 0)
m = –1 (∆Gp < 0)
Note that no efficiency correction (e) is required for the ∆Gc term because ∆Gc is already defined in terms of ATP energy required for synthesis. Inefficiencies have been empirically included. But not so for ∆Gp.
Substituting into our earlier equation results in the following:
Heterotrophic Growth — Ammonia as N-Source
Eq (1)

m = +1 (∆Gp > 0)
m = –1 (∆Gp < 0)
in which e = 0.6 and ∆Gc = 7.5 kcal are usually assumed. Equation (1) is exactly as McCarty
derived it.1-4
C. Estimating Yield Coefficients
Recall that the model we generally employ for microbial growth has the following form:
dXa/dt = Y(dF/dt) – bXa
where Y represents the stoichiometric relation between gross growth and substrate utilization. Strictly speaking, Y ignores decay and/or maintenance. Likewise, the ATP balance employed to estimate A-values (eeq e.d. to energy per eeq cells synthesized) also ignores decay and/or maintenance.
A-values can easily be used to estimate microbial yield coefficients (Y-values). In formation of 1 eeq cells, A eeq of e.d. is used for energy while 1 eeq of e.d. is used for synthesis. Consequently,
Eq (2)
![]()
where ae is really a yield coefficient based on electron equivalents, rather than usual units (g VSS per g COD or BODL)[Note: COD = chemical oxygen demand; BOD = biochemical oxygen demand; BODL = ultimate biochemical oxygen demand]. We can convert to conventional units by noting that 1 eeq cells = 5.65 grams of cellular VSS (4.04 grams, if NO3– is N-source); and 1 eeq of e.d. = 8 grams of COD. Therefore,
Ammonia as N-source
Eq (3)
![]()
Example — Heterotrophic Growth
Suppose we are interested in the aerobic utilization of acetate, with ammonia as N-source:
e.d = acetate
e.a. = O2
N
= NH4+
Consulting Table 1:
∆Gr = Rxn (11) – Rxn (3) = –6.609 – (18.675) = –25.284 kcal
∆Gp = Rxn (11) – Rxn (16) = –6.609 – (–8.545) = +1.936 (--> m = +1)
∆Gn = 0
![]()
![]()
which compares remarkably well with a measured value of 0.410 g VSS/g COD [Burkhead, C.E., and R.E. McKinney, “Energy Concepts of Aerobic Microbial Metabolism,” Proc. Amer. Soc. Civil Engrs, 95 (SA2) 253 (1969)]. However, it should be noted that measured values are notoriously imprecise — seek long enough, and you will find whatever number you like!
McCarty2,4 has tabulated comparisons between ae values estimated using his bioenergetics approach, and ae values estimated from microbial yields reported in the literature (Table 2).
While there are certainly discrepancies in Table 2 between thermodynamically predicted ae values and reported ae values, there is generally sufficiently good agreement to encourage the use of Equations (1) and (2) in situations where experimental data are either lacking or unreliable.
TABLE 2. VALUES OF ae FOR HETEROTROPHIC REACTIONS*
(Ammonia as N-source)
ae
eeq of cells per eeq electron donor consumed
Electron Electron Estimated from Estimated from
Donor Acceptor Reported Values Thermodynamics**
Glucose O2 0.79 0.72
Benzoate O2 0.46 0.60
Propionate O2 0.58 0.59
Acetate O2 0.58 0.59
Alanine O2 0.52 0.64
Methanol CO2 0.15 0.21
Benzoate CO2 0.11 0.062
Glucose CO2 0.27 0.28
Propionate CO2 0.069 0.048
Acetate CO2 0.06 0.047
* Excerpted
from Reference [4].
** Equations (1) and (2), with e = 0.6; ∆Gc = 7.5 kcal/eeq
D. Stoichiometry
When the same electron donor is used for synthesis and energy production (as is usually — but not always — the case in heterotrophic metabolism), it is easy to arrive at “growth equations” which specify the stoichiometries involved. These equations are very useful for such things as predicting nutrient requirements, alkalinity changes, gas compositions, and other factors associated with microbial activities. Our stoichiometries will even include decay.
In general, we may write a growth stoichiometry as the sum of synthesis and energy reactions:
Synthesis:
fs (edred + N-source ---> edox + cells)
Energy:
fe (edred + eaox ---> edox + eared)
where
fs = fraction of e.d. to net synthesis (i.e., including all biologically formed VSS — Xa as well as the inert remains of decayed cells);
fe = fraction of e.d. to energy;
edred, edox = reduced and oxidized forms of the e.d., respectively;
eared, eaox = reduced and oxidized forms of the e.a., respectively.
Note that fs + fe = 1, and that fs and fe are functions of SRT ("theta_c") as well as A.
Define:
Rd = half-reaction for oxidation of the e.d.;
Ra = half-reaction for formation of the e.a.;
Rc = half-reaction for oxidation of cells.
These are all defined as oxidations, as per Table 1. Half-reaction Rc is either Rxn (1) or (2), depending upon the N-source.
Our general stoichiometry may be written as follows:
Eq (4)
Rd – fe Ra – fs Rc
At first glance, Equation (4) may not look like an equation; but each of its components (Rd, Ra, and Rc) are chemical equations (half-reactions). Thus, Equation (4) is really a recipe for doing “equation arithmetic,” with a resulting equation which is a linear combination of three half-reaction equations.
We next need to derive the functional relationship, fs = f(A, theta_c). We can do so by simple extension of our earlier efforts at modeling MLVSS. We know that the effective yield (Yobs) of biologically formed VSS (active + inert remains of decayed cells) is given by:
![]()
Similarly, fs is the effective yield of biomass (eeq) — living and dead — per eeq of e.d. consumed. It is the “eeq analog” to Yobs. The “eeq analog” to Y is ae. Therefore, by analogy,
Eq (5)
![]()
The relationship between fs, fe, and theta_c is shown below.

Note how the fraction of e.d. going to synthesis decreases with theta_c from a value of ae at theta_c = zero, to an asymptote of 0.2ae. (At infinite theta_c, Xa --> 0, and all biological solids consist of the inert remains of decayed cells.) Also note that real reactors cannot function below some minimum theta_c, so the portion of the curve at very low theta_c values at is merely hypothetical.
Example — Aerobic Utilization of Acetate
This is a continuation of an earlier example (page 17). Suppose we are interested in the aerobic utilization of acetate, with ammonia as N-source:
e.d = acetate
e.a. = O2
N
= NH4+
theta_c = 8 days; b = 0.1 day-1.
From earlier example, A = 0.707 eeq to energy per eeq cells formed.

Rd:
0.125
CH3COO– + 0.375 H2O ---> 0.125 CO2 + 0.125 HCO3– + H+ + e–
–feRa:
0.155 O2 + 0.622 H+ + 0.622 e– ---> 0.311 H2O
–fsRc:
0.0756 CO2 + 0.0189 HCO3– + 0.0189 NH4+ + 0.378 H+ + 0.378 e–
---> 0.0189 C5H7O2N + 0.170 H2O
0.125 CH3COO– + 0.155 O2 + 0.0189 NH4+
---> 0.0494 CO2 + 0.106 HCO3– + 0.106 H2O + 0.0189 C5H7O2N
Which tells us that 0.125 mol acetate (= 1 eeq = 8 g COD) will result in 0.0189 mol of C5H7O2N (= 0.0189 mol . 113 g VSS/mol = 2.14 grams of biologically produced VSS). Thus, the observed yield, Yobs= 2.14 ÷ 8 = 0.267 g VSS/gCOD. This should, of course, agree with the number arrived at via
![]()
The stoichiometric equation is useful for estimating N requirements, P requirements (recognizing that P is required in a mass amount which is 1/5 of the mass of N required for synthesis, or about 100(1/5)(14/113) = 2.5% of biologically formed VSS). You can get the same information without bothering to derive the whole stoichiometry — by applying Yobs∆S to estimate VSS production, and then using knowledge of biological solids composition (C5H7O2N) to estimate N, P requirements. But the stoichiometry provides other potentially useful information, such as alkalinity and CO2 production/consumption. This additional information — unavailable from application of Yobs alone — may be important in predicting pH effects and in designing buffer systems for biological reactors.
Example — Mixed Substrate
A complex wastewater has a BODL of 400 mg/L which is 75% carbohydrate, 15% grease, and 10% protein (all on a BOD basis). Based upon bioenergetic principles, estimate Y applicable to aerobic treatment (assuming NH4+ as N-source).
In such a case, the overall Y is merely the weighted average of the Y-values for each of the three components:
Carbohydrate
∆Gr = Rxn (9) – Rxn (3) = –10.0 –18.675 = –28.675 kcal/eeq
∆Gp = Rxn (9) – Rxn (16) = –10.0 +8.545 = –1.455 kcal/eeq
(--> m = ‑1)

![]() eeq cells/eeq
carbohydrate
eeq cells/eeq
carbohydrate
Grease (Fats and Oils)
∆Gr = Rxn (10) – Rxn (3) = –6.6 –18.675 = –25.275 kcal/eeq
∆Gp = Rxn (10) – Rxn (16) = –6.6 +8.545 = +1.945 kcal/eeq
(--> m = +1)
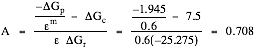
![]() eeq cells/eeq
grease
eeq cells/eeq
grease
Protein
∆Gr = Rxn (8) – Rxn (3) = –7.7 –18.675 = –26.375 kcal/eeq
∆Gp = Rxn (8) – Rxn (16) = –7.7 +8.545 = +0.845 kcal/eeq
(--> m = +1)

![]() eeq cells/eeq protein
eeq cells/eeq protein
Mixture

Ymix = (5.65/8) ae = 0.489 g Xa/g BODL
A stoichiometry for this waste’s degradation can be estimated as follows: First, determine stoichiometries for each of the three components (on a 1 eeq e.d. basis each) as usual; multiply each stoichiometry by the appropriate fractional contribution which the component makes to total BODL; and then add the weighted stoichiometries together to provide an estimate for the mixture.
BIBLIOGRAPHY
1. McCarty, P.L., "Energetics and Bacterial Growth," presented at the 5th Rudolf Research Conference, Rutgers, the State University, New Brunswick, New Jersey, July 2 (1969).
2. McCarty, P.L., "Stoichiometry of Biological
Reactions," presented at the
International Conference, "Toward a Unified Concept of Biological Waste
Treatment Design," Atlanta,
Georgia, October 6 (1972).
3. McCarty, P.L., “Energetics and Bacterial Growth,” in S. D. Faust and J. V. Hunter (ed.), Organic Compounds in Aquatic Environments, Marcel Dekker, Inc., New York, pp. 495-512 (1971).
4. McCarty, P.L., “Stoichiometry of Biological Reactions,” Progr. Water Technol., 7, 157-172 (1975).
5. McCarty, P.L., “Energetics of Organic Matter Degradation,” chapter 5 in Mitchell, R. (ed.) Water Pollution Microbiology, 91-118, John Wiley & Sons (1972).
6. McCarty, P.L., “Thermodynamics of Biological Synthesis and Growth,” The Proceedings of the 2nd International Water Poll. Research. Conf., Tokyo, 1964. Pages 169-199, Pergamon Press (1965).