Evaluation of Method

Evaluation of The Method: Comparing Estimated and Measured %ABV

Evaluation of The Method: Comparing Estimated and Measured %ABV

My refractometer-based method for estimating %ABV from pre- and post-fermenation Brix was evaluated using a dataset of 12 beers. Results were compared to experimentally measured %ABV data. Note that most of my brewing is of fairly high-gravity beers – Northern Ale, Double IPA (DIPA), Honey Malt Ale, Belgian Tripel; consequently, the dataset is skewed towards the high end of %ABV. There is also one apple cider among the set. Two of the samples (DIPA-1a and 1b) were actually of the same beer, sampled months apart.

%ABV

Figure 1 presents comparison of Brix-estimated vs. measured %ABV.

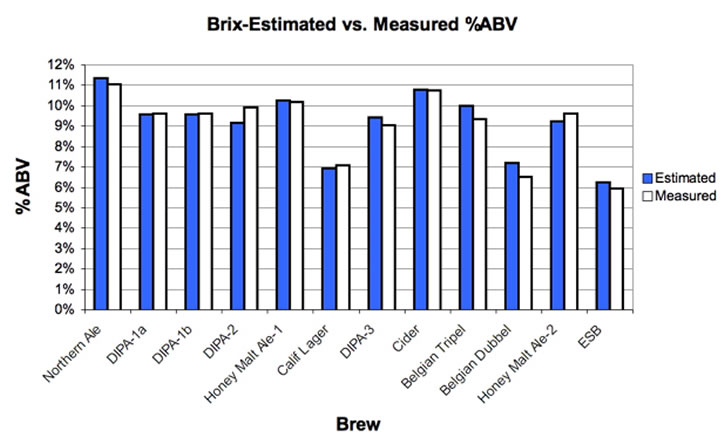
AppleMark

Figure 1. Comparison of Brix-based modeled vs. measured %ABV for a dataset of 12 brews.

The summary statistics are: mean difference = 0.1 %ABV; sample standard deviation of the difference (n=12) = ±0.4 %ABV. Thus, one can reasonably expect to estimate %ABV, for home-brewing purposes, with the Brix-based calculator. Commercial brewers would likely feel the need for more accuracy.

The mean difference and sample standard deviation of the difference reflect some combination of imprecision and inaccuracy – in both the model-based estimates and in the experimental measures of %ABV. We are comparing the model-based estimates to imperfect measures of “actual %ABV.” As reported earlier, the standard deviation of the method used here for measuring alcohol content is ± 0.2 %ABV. And imprecision in reading the Brix scale affects model estimates of %ABV, just as it does experimental measures of %ABV: the refractometer cannot be read more precisely than to ± 0.1 Brix. That sort of imprecision in reading the Brix scale propagates to an imprecision in model-estimated alcohol values of about 0.1% ABV. Putting these sources together, it’s not hard to understand why imprecision in the difference between Brix-estimated model and measured alcohols would be as high as ± 0.4% ABV.

Residual Real Extract

Figure 2 presents Brix-based calculator estimates of residual Real Extract (P_f) versus “measured” values.

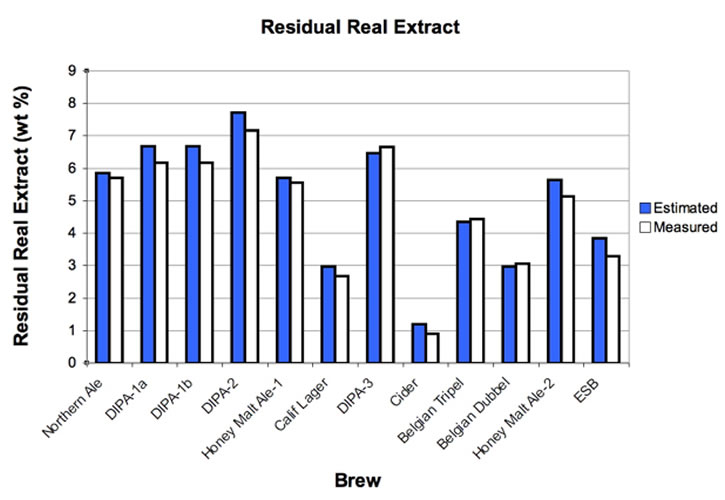
AppleMark

Figure 2. Comparison of Brix-based modeled vs. “measured” residual real extract.

What I am referring to as “measured” residual RE is not quite that. It’s not based on specific analysis of carbohydrates, via HPLC or some wet-chemical technique (e.g. anthrone reagent). As presented elsewhere, it is based on Brix measurement (B_f _{aft boil/reconst}) of the beer after boiling off 75-80% of its volume (to remove EtOH) and replacing it with distilled water. If we assume that the factor of 1.04 between initial Brix (B_i) and initial extract (P_i) in pre-fermented wort represents non-carbohydrate constituents that contributed to initial Brix; and that these remain after fermentation; then

residual RE _“meas” = B_f _{aft boil/reconst} – (B_i –B_i/1.04)*(OG/SG_f _{aft boil/reconst})

The factor (B_i –B_i/1.04) represents the grams of non-carbohydrate contribution to original Brix (B_i) and the ratio (OG/SG_f _{aft
boil/reconst}) corrects for the difference in specific gravity between original, pre-fermentation wort (when the B_i measurement was made) and the specific gravity of the post-fermentation beer after boil/reconstitution (when the B_f _{aft boil/reconst} measurement was made). It is necessary because the reference on which weight% is based has changed. The same mass of nonfermentable carbohydrates in 100 g of original wort at (for example) SG = 1.050 will contribute a greater extent of weight% to a post-fermentation beer, after boil/reconstitution, with (for example) SG =1.010.

The model-estimated residual RE compares reasonably well with the “measured” residual RE.

Final Brix, After Boiling/Restoration

For those who would prefer to model the final Brix measured on the post-fermentation beer, after boiling off 75-80% of its volume and restoring with distilled water, I present Figure 3.

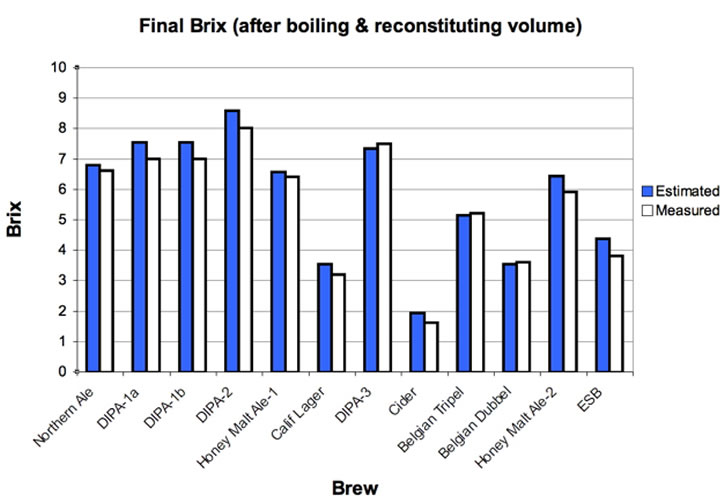
AppleMark

Figure 3. Comparison of Brix-based modeled vs. measured residual Brix (after boiling/reconstitution).

Comparison With Hydrometer-Based Methods of %ABV Estimation

There are many hydrometer-based methods to estimate %ABV in finished beers. I chose only four of them for comparison to my Brix-based method.

Standard SG-Drop Method

From the FermCalc website

http://web2.airmail.net/sgross/fermcalc/fermcalc_alcohol.html

“…Described on pages 79-80 of First Steps in Winemaking by C. J. J. Berry (1987). It estimates the alcohol content by dividing the drop in specific gravity by the constant 0.00736,” or:

a_v = (sg_i - sg_f) / 0.00736

where

a_v = alcohol content, % by volume
sg_i = initial specific gravity
sg_f = final specific gravity

Miller

From Dave Miller (The Complete Handbook of Homebrewing, 1988, Storey Communications. Miller uses the same formula as the Standard, SG-Drop Method above, except the factor in denominator is 0.0075.

Duncan and Acton

From the FermCalc website

http://web2.airmail.net/sgross/fermcalc/fermcalc_alcohol.html

“This method is described on pages 64-66 of Progressive Winemaking by Peter Duncan and Bryan Acton (1967).”

a_v = 1000(sg_i - sg_f) / [7.75 - 3.75(sg_i - 1.007)]

Realbeer.com

http://www.realbeer.com/library/beerbreak/archives/beerbreak0301.php

Gives %ABW

ABW = 76.08(OG-FG)/(1.775-OG)

which I then converted to %ABV by %ABV = %ABW*FG/0.794, where 0.794 is the density of EtOH at 15˚C.

I used each of the four hydrometer-based methods to estimate %ABV in the 12 finished beers. Because my FG hydrometer measurements were made on finished, bottle-conditioned beer, I added 0.0036 to OG (pre-fermentation) hydrometer measurements to include the effects of 5 oz/gal bottling sugar.

Figure 4 presents the results, with both my Brix-based, model predictions and measured %ABV shown for comparison.

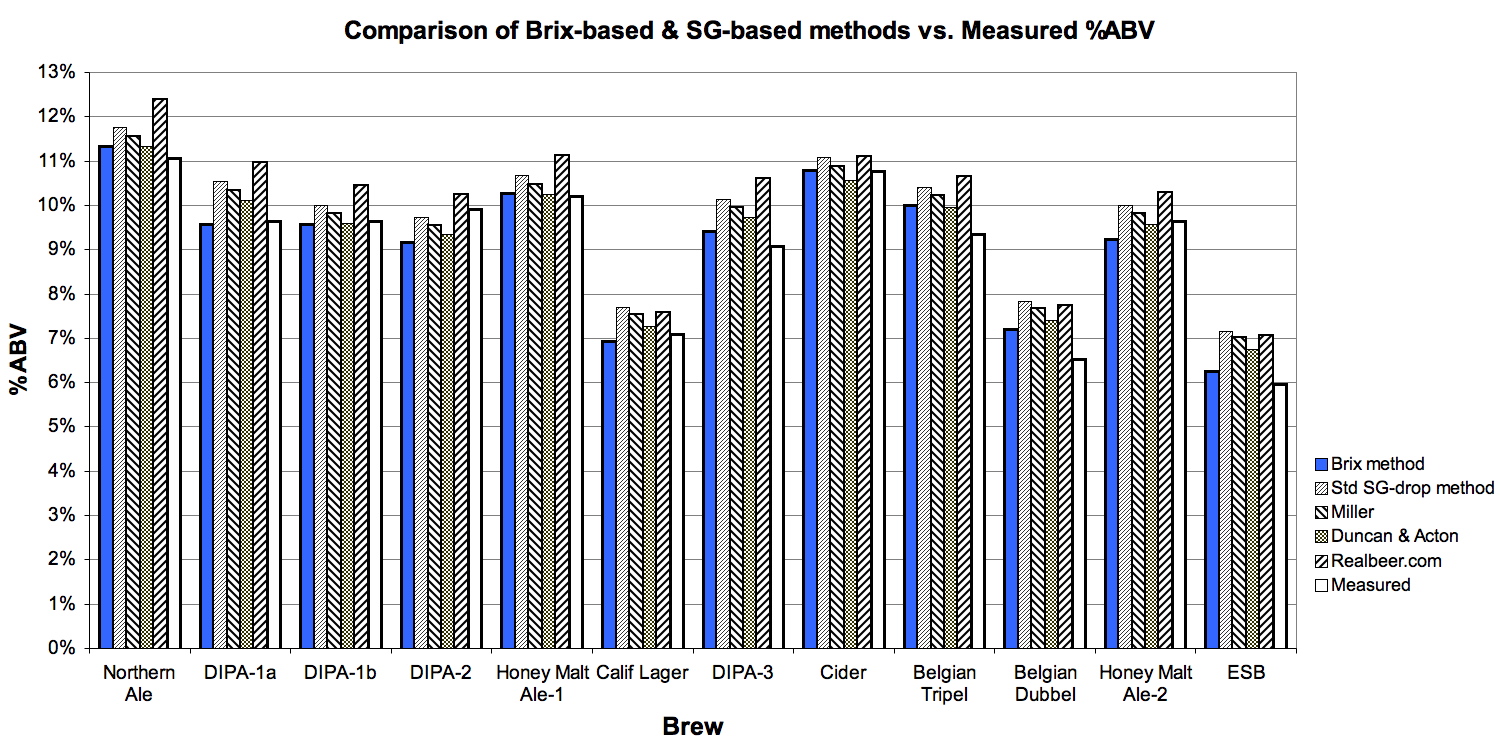
Figure 4. Comparison of Brix-based method and four hydrometer-based methods with measured %ABV,

If the measured %ABV values are to be believed, the Brix-based method appears at least as accurate as any of the hydrometer-based methods.

The data are presented in an alternative way in Figure 5.

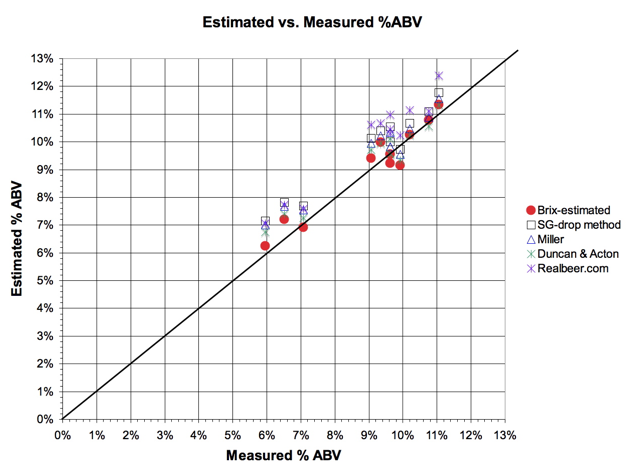
AppleMark

Figure 5. Scatter plot of estimated vs. measured

The four, hydrometer-based methods tend to over-estimate %ABV. As presented earlier, the mean error (from measured %ABV) of the Brix-based method was +0.1 %ABV, with sample standard deviation (n=12) of ±0.4 %ABV.

It is, of course, up to prospective users whether this level of accuracy and precision is sufficient for their needs. However, consider that similar analysis of most hydrometer-based methods is not readily available.

Derivation of Calculator Equations