Stoichiometry of Maltose Fermentation to Ethanol

© James M. Gossett (March 25, 2012) Questions/Comments?

Overview
Stoichiometry of Ethanol Production From Maltose
Contribution of Ethanol to Apparent Brix
Measurement of %ABV Using Brix Refractometry
Derivation of Calculator Equations
Evaluation of The Method: Comparing Estimated and Measured %ABV

---

Consideration of two factors is required to estimate ethanol (EtOH) production from initial and final refractometer (Brix) measurements:

(i) the stoichiometry of maltose fermentation to EtOH; and

(ii) the contribution that the resulting EtOH makes to Brix.

In this section, the stoichiometry is considered.

Wort is a complex mixture of carbohydrates, but I will simplify by assuming that the major fermentable fraction is maltose, C₁₂H₂₂O₁₁ (FW = 342 g/mol). Carbohydrate composition certainly varies among beer-types, but maltose is by far the sugar at highest concentration in most worts, constituting about 50% of wort carbohydrate.¹⁰ Given that wort carbohydrate is only about 65% to 75% fermentable (and maltose is 100% fermentable), then maltose certainly constitutes far more than 50% of the fermentable carbohydrate fraction of wort. The next highest sugar fractions are glucose and maltotriose, which are generally each present at only about 1/5^th the levels of maltose. [See Table 2.3 in Boulton and Quain.¹⁰] Since maltose (a disaccharide) has a chain-length midway between glucose (a monosaccharide) and maltotriose (a trisaccharide), that also makes it a particularly good stand-in for the fermentable extract of wort.

Balling’s Equation

Carl J. N. Balling^1,2 observed the following stoichiometry:

2.0665 g fermentable extract ---> 1 g EtOH + 0.9565 g CO₂ + 0.11 g losses Eq [1]

Assume “fermentable extract” = maltose, and that “losses” are settled biomass from yeast synthesis (which I will represent as total suspended solids, TSS).

Balling’s studies date from 1843 -1865, but his stoichiometry has stood up reasonably well. It is established^3,4 that Balling’s stoichiometry somewhat under-predicts ethanol production; or, put another way, using it in reverse to predict original extract (OE, original gravity in degrees Plato) for a given %ABW tends to over-predict OE. Several modern researchers^3,4 have raised theoretical objections to Balling’s stoichiometry — e.g., that evaporations of water and alcohol are ignored; that net losses from yeast growth differ significantly between lagers and ales; that Balling's CO₂ values are assumed (1 mol CO₂ per mol EtOH) and not measured; and that not all CO₂ produced will be evolved (some will remain dissolved in the wort]). Nonetheless, tinkering with Balling’s equation has ultimately resulted in remarkably marginal improvements.

For example, after lengthy, comprehensive analysis of large datasets, followed by derivation of new equations, Cutaia et al. concluded,³ “Nonetheless, it is tribute to the analytical skills of Balling that he could determine the Balling constants … in the mid-1800s. The original Balling values are embedded in the brewing literature and their use … is reported to slightly overestimate the original extract. Application of Balling’s original equation to the datasets in this paper similarly overestimates original wort extract in all datasets but one. However, OE, RE and OH_ww measurement errors may overshadow differences in the Balling constants. For these reasons and since the Balling equation is embedded in the brewing literature (and culture!) we do not expect (nor recommend) adaptation of a new Balling equation.”

Bioenergetics & Stoichiometry: Another Approach

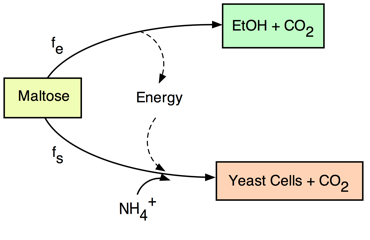
Yeast use maltose as both carbon source for synthesis of new yeast cells, and as electron donor for energy production. Energy is required for synthesis of new cells from maltose, and yeast derive that energy from fermentation of maltose to EtOH under anoxic conditions. Thus, we can consider that a fraction, f_e, of maltose is used for energy; and a fraction, f_s, is used for synthesis. Note that f_s + f_e = 1.

Energy reaction

Eq [2]

Synthesis reaction

To write a synthesis reaction, converting maltose to yeast cells, we must have a model for the composition of yeast. Here we are presented with some difficulty: composition varies significantly with species, strain, growth conditions, and stage of fermentation (i.e., early vs. late).^10,12

Simmonds,¹² in averaging a number of different sources, reported the organic portion (dry weight basis) of yeast is about 90% of total dry weight, and in terms of major elements, the organic portion is 48.3% C, 6% H, 34.5% O, and 10.6% N. This translates to a molar formula for the major elements in the organic fraction of yeast of C_4.03H₆O_2.16N_0.76 (MW = 99.56 g/mol). Given the oxidation states of H (+I), O (–II), and N(–III)[i.e., protein], such a formula suggests that the average oxidation state of carbon is +0.149. It also means that in carbonaceous oxidation of yeast to CO₂ (producing +IV carbon), the number of electrons evolved would be: 4.03*(+4 - 0.149) = 15.52 for C_4.03H₆O_2.16N_0.76. Thus, 1 electron equivalent (eeq) of yeast would be (1/15.52)*99.56 = 6.41 g VSS or about 6.41/0.9 = 7.12 g TSS. [Note: VSS = volatile suspended solids, a standard measure of organic particular matter; TSS = total suspended solids, a standard measure of total particulate matter (organic + ash).]

Rosen¹¹(cited in Boulton and Quain¹⁰) reported an elemental model for yeast VSS of C_4.02H_6.5O_2.11N_0.43P_0.03. Let’s ignore the phosphorus content, as being much smaller than the content of the other elements, giving C_4.02H_6.5O_2.11N_0.43 (MW = 94.52 g/mol). This implies the average oxidation state of carbon is –0.246. [Note the more reduced state of carbon than if the empirical formula of Simmonds is used, owing to the significantly lower nitrogen content in Rosen’s formula.] In carbonaceous oxidation to CO₂ (+IV carbon), the number of electrons evolved would be: 4.02*(+4 + 0.246) = 17.07 for C_4.02H_6.5O_2.11N_0.43. Thus, 1 eeq of yeast would be (1/17.07)*94.52 = 5.54 g VSS or about 5.54/0.9 = 6.16 g TSS.

An often-used⁹ empirical formula for the elemental content of microbial biomass is C₅H₇O₂N (113 g/mol). This wasn’t intended so much for yeast as for bacteria. In this formula, the average oxidation state of carbon is zero – i.e., between those of the models of Simmonds (+0.149) and Rosen (–0.246). The number of electrons evolved in carbonaceous oxidation of C₅H₇O₂N would be 20. Thus, 1 eeq of C₅H₇O₂N would be (1/20)*113 = 5.65 g VSS or about 5.65/0.9 = 6.28 g TSS. This is slightly higher than Rosen’s formula would predict (6.16 g TSS), but lower than Simmonds’ (7.12 g TSS).

Conclusion: Given that yeast composition can vary significantly depending upon strain and growing conditions, there is little to recommend against the use of C₅H₇O₂N as an empirical formula for the ratio of major elements in the organic fraction of yeast. Though it was formulated to model the principal elements in the organic fraction of bacterial biomass, I am using it here to approximate the organic solids of yeast cells. It is an assumption positioned between the sources^10,11,12 consulted on yeast composition.

Thus, the two half-reactions that are combined to produce a reaction for synthesis of yeast cells from maltose are as follows:

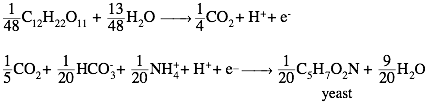
If we keep only the relevant terms and normalize to one mole of maltose, the synthesis reaction becomes

Eq [3]

Yeast cells (dry weight basis) are about 90% organic matter, 10% inorganic matter. Since the formula weight of C₅H₇O₂N is 113 g/mol, the 2.4 moles of C₅H₇O₂N appearing on the right-hand side of the synthesis reaction corresponds to 2.4(113)/0.9 = 301.3 g total suspended solids (TSS).

Complete Stoichiometry (combined energy and synthesis reactions)

The complete stoichiometry for maltose fermentation is thus given by:

f_e*Eq[2] + (1 – f_e)*Eq[3] Eq [4]

Our quest, then, becomes estimation of f_e, the net fraction of maltose used for energy in fermentation of wort.

McCarty^5-9 developed a method that uses bioenergetics (based on thermodynamic data and observations about microbial efficiencies of energy capture and utilization) to estimate cellular yields from substrate degradation. With estimates of specific decay/maintenance rate, the method allows f_e to be estimated. For those readers who are familiar with the method (e.g., students in my CEE6570 Biological Processes graduate class at Cornell University), details are provided in the following. Readers unfamiliar with the method will undoubtedly be lost;  a tutorial is presented here.

∆G⁰(W), kcal

R_d: –10.0

R_a: +7.592

∆G_r = 2.408 kcal

∆G_p = –1.455 kcal

Both a_e and Y are gross yields (albeit in different units), uncorrected for maintenance/decay, which should be appreciable in prolonged fermentation. Without such corrections, a_e is the same as f_s, the fraction of malt used in biosynthesis; this means, uncorrected for maintenance/decay, bioenergetics predicts f_e = 1 – f_s = 0.82 (clearly too low).

A rational approach to correct for maintenance/decay: Consider that most of the yeast growth occurs in the first few days, followed by autolysis ("endogenous decay") over an extended, batch fermentation period.  As reasonable values, let's choose a specific decay rate, b = 0.02 d^-1 and a fermentation period of 30 days.  The basis for selecting the decay rate is that 2% per day is typical for anaerobic processes at sub-ambient temperatures.  The basis for selecting a period of 30 days? That's a typical fermentation period.  Obviously, both decay rate and fermentation period would be temperature-dependent, but in opposite directions (i.e., decay rate would increase with temperature, while fermenation period would decrease with temperature).  Thus, their product is relatively insensitive to temperature, and it's the product bt that appears in the relevant equation.

Considered as an extended batch process (t= 30 d, b = 0.02 d^-1)

f_s = a_e exp(–bt) = 0.179 exp[–0.02(30)] = 0.10

------> f_e = 0.90

Its use with Eq [4] gives the following stoichiometric relationship:

1 g maltose ---> 0.484 g EtOH + 0.494 g CO₂ + 0.088 g TSS Eq [5]

Comparison With Balling’s Equation

Expressed per g maltose fermented, Balling’s equation, Eq [1], becomes

1 g maltose ---> 0.4839 g EtOH + 0.4629 g CO₂ + 0.0532 g TSS Eq [6]

What value of f_e used in Eq [4] corresponds to Balling’s observations? The following Table was created for different assumed values of f_e:

	Per gram maltose consumed
fe	g EtOH	g CO2	g TSS
0.90	0.484	0.494	0.088
0.91	0.490	0.496	0.079
0.92	0.495	0.498	0.070
0.93	0.500	0.500	0.062
0.94	0.506	0.502	0.053
0.95	0.511	0.504	0.044
0.96	0.516	0.506	0.035
0.97	0.522	0.508	0.026
0.98	0.527	0.511	0.018
0.99	0.533	0.513	0.009
1.00	0.538	0.515	0.000
	makes EtOH agree with Balling
	makes TSS agree with Balling

It can be seen that no single value of f_e will give agreement with Balling for all three products (EtOH, CO₂, and TSS). In fact, no reasonable value of f_e allows agreement for CO₂. Since Balling’s CO₂ value was clearly based on the assumption of equal moles EtOH and CO₂ produced in fermentation (rather than being based on actual measurement), there is no reason we should concern ourselves with fitting it. Because Balling ignored the net CO₂ that will be produced in synthesis of cells from maltose (Eq[3]), Balling’s equation is necessarily going to underestimate CO₂ produced per gram maltose. On the other hand, not all CO₂ produced will be evolved (lost) from the beer; some will remain dissolved. Balling’s theoretical underestimation of CO₂ production might unintentionally correct (somewhat) for this. Nonetheless, Balling’s underestimation of wort losses (CO₂ and settled yeast cells) could, in part, explain his stoichiometry’s tendency to underestimate ethanol production (%ABW): if wort losses are underestimated, then final gravity is overestimated, lowering estimated EtOH weight percentage because the denominator (total final wort mass per 100 g initial wort mass) has been overestimated.

Conclusion

So, what value of f_e am I going to use? In the end, I elected to use a value consistent with both the bioenergetics analysis and with Balling’s EtOH observations, since predicting EtOH production is my main objective:

---------> f_e = 0.90

This is the value employed in my Brix-based, %ABV calculator. Its use gives the following stoichiometric relationship:

1 g maltose ---> 0.484 g EtOH + 0.494 g CO₂ + 0.088 g TSS Eq [5]

Eq [5] differs from Balling’s, Eq [6], in the following manner: My stoichiometry predicts greater CO₂ evolution than Balling’s, since he ignored CO₂ evolved from cell synthesis; and my stoichiometry predicts greater cell synthesis. Since only 10% of maltose is used in synthesis, these differences in stoichiometry are not very important. Furthermore, they only come into play in estimating final wort mass through subtraction of evolved CO₂ and settled biomass solids from initial wort mass. Since most of the wort mass is water, these stoichiometric differences in estimated losses of CO₂ and biomass solids are not very important. It is, however, more theoretically satisfying to make these changes: there is no theoretical justification for ignoring CO₂ evolved in synthesis.  It is also satisfying that application of bioenergetics can predict a value of f_e in reasonable agreement with Balling's observations.   In all this, it should be noted that I am walking in the footsteps of other researchers who have raised theoretical objections to Balling, but who have, in the end, not improved significantly upon his work.^3,4

References & Resources

1. Balling, Carl. J. N., Die Bierbrauerei. Verlag von Friedrich Temski: Prague, CHZ, 1865.

2. Balling, Carl J. N. “Die Gärungschemie” I-IV, Prague 1845, “Die Gärungschemie” I-III. 2. Aufl., Prague 1854, “Lehrbuch der Bierbrauerei” I-II, 3. Aufl. Prague 1865.

3. Cutaia, A. J., A-J Reid, and R. A. Speers. “Examination of the relationships between original, real and apparent extracts, and alcohol in pilot plant and commercially produced beers,” Journal of the Institute of Brewing, 115(4), 318-327 (2009).

4. Neilson, H., A. G. Kristiansen, K. M. Krieger Larsen, and C. Erikstrom. “Balling’s formula - scrutiny of a brewing dogma,” Brauwelt Int., 25, 90-93 (2007)

5. McCarty, P. L., “Energetics and Bacterial Growth,” in S. D. Faust and J. V. Hunter (ed.), Organic Compounds in Aquatic Environments, Marcel Dekker, Inc., New York, pp. 495-512 (1971).

6. McCarty, P. L., “Stoichiometry of Biological Reactions,” Progr. Water Technol., 7, 157-172 (1975).

7. McCarty, P. L., “Energetics of Organic Matter Degradation,” chapter 5 in Mitchell, R. (ed.) Water Pollution Microbiology, 91-118, John Wiley & Sons (1972).

8. McCarty, P. L., “Thermodynamics of Biological Synthesis and Growth,” The Proceedings of the 2nd International Water Poll. Research. Conf., Tokyo, 1964. Pages 169-199, Pergamon Press (1965).

9. Rittmann, B. E., and P. L. McCarty, Environmental Biotechnology: Principles and Applications, McGraw-Hill, New York, NY (2001).

10. Boulton. C. and D. Quain, Brewing Yeast & Fermentation. Oxford, U. K., Blackwell Science Ltd. (2001).

11. Rosen, K. “Preparation of yeast for industrial use in the production of beverages.” In Biotechnological Applications in Beverage Production (eds C. Cantarelli and G. Lanzarini), pp. 164-223. Elsevier Science Publishers, New York (1989).

12. Simmonds, C., Alcohol, Its Production, Properties, Chemistry, And Industrial Applications. Macmillan & Co. (1919).

Overview Contribution of EtOH to Brix; Measurement of %ABV